In diesem Blog schreibt Marcus Seuser, Master-Student der Humangeographie und Geoinformatik an der Universität Tübingen, über sein Forschungsprojekt zum Brexit und stellt dabei die ArcGIS Werkzeuge zur räumlichen Regression vor.
Mit räumlicher Regression nach dem Warum fragen
Wer schon einmal eine Hot-Spot-Analyse durchgeführt hat, weiß um das Potential dieser Werkzeugklasse, wenn es darum geht Hypothesen zur räumlichen Verteilung von Ereignissen zu verifizieren. Das Wo steht hierbei im Vordergrund. Gibt es wirklich ein Viertel, in dem deutlich mehr Hauseinbrüche stattfinden? Ist der Anteil an Diabeteskranken in einem Landesteil signifikant höher als in anderen? Ich will in diesem Blogartikel noch eine Ebene tiefer gehen und nach den Gründen für Ereignisse fragen, dem sich logisch anschließenden warum. Welche Faktoren sind für die Verteilung von Phänomenen verantwortlich? Und welche Ursache ist am gewichtigsten?
ArcGIS bietet hierfür eine eigene Toolbox, die sich Modeling Spatial Relationships nennt. Hierzu gehören multivariate Regressionsanalysen und die eigens für räumliche Fragestellungen entwickelte räumlich gewichtete Regression. Bevor ich einen großen Teil meiner Leser jetzt verliere: Ja, es geht um Statistik. Nein, es wird keine weitreichende Formelsammlung geben und es soll hauptsächlich darum gehen, einen grundsätzlichen Workflow vorzustellen. Welche Fallstricke existieren, wie interpretiere ich diagnostische Werte, wie kalibriere ich mein Modell und welche Aussagekraft hat es schließlich? Ich werde dies anhand eines eigenen Forschungsprojekts vorstellen, in welchem ich die Ursachen für das Wahlverhalten im Fall Brexit beleuchte.
Der Brexit und einige Erklärungsversuche
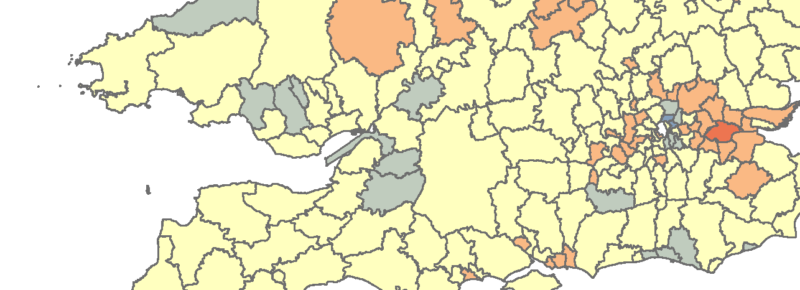
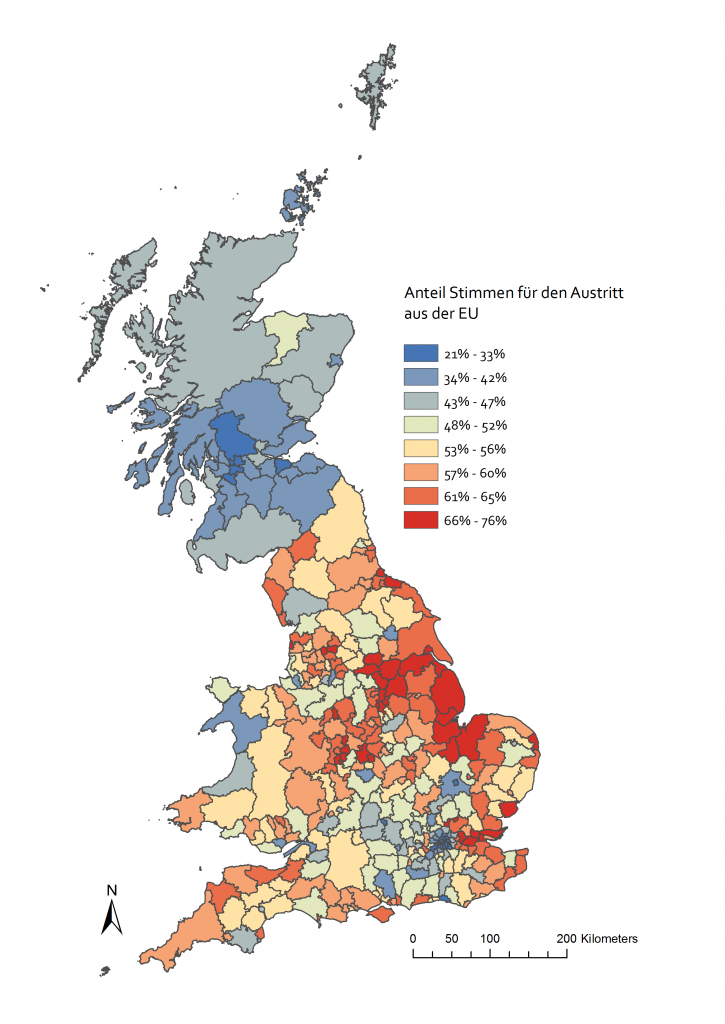
Im Zuge eines Referendums am 23. Juni 2016 stimmten 51,9 % der Briten für einen Austritt aus der Europäischen Union. Für viele Beobachter war dieses Ergebnis ein Schock und in den anschließenden Tagen waren die Medien voll von Vermutungen, welche strukturellen Ursachen verantwortlich wären. Wie in Abb. 1 zu sehen ist, war Großbritannien in hohem Maße durch das Referendum gespalten worden. Schottland, der Großraum London und einige weitere Großstädte hatten mit großer Mehrheit für einen Verbleib in der EU gestimmt, während ein Großteil der Distrikte im Osten für den Austritt gestimmt hatte. Als mögliche Begründungen wurden das unterschiedliche Bildungsniveau, ein ungleiches wirtschaftliches Wachstum sowie die Altersverteilung im jeweiligen Distrikt angeführt. Unsere wissenschaftliche Fragestellung lautet nun: Besteht ein Zusammenhang zwischen den Abstimmungsergebnissen und den aufgezählten Einflussgrößen, welche hat die größte Bedeutung und gibt es regionale Unterschiede?
Um diese Fragestellung mit einer Regressionsanalyse zu lösen, muss sie zuerst in eine Formel „gegossen“ werden. Der grundsätzliche Aufbau ist für alle Untersuchungen gleich.
![]()
y ist unsere abhängige Variable „Anteil der Bürger für EU-Austritt“. Die Koeffizienten β zeigen an, welchen Einfluss die unabhängigen Variablen x auf die Ausprägung von y haben. ε enthält schließlich die Residuen, den Anteil der Ausprägungen von y, den die Variablen nicht erklären können. Im nächsten Schritt müssen die Annahmen operationalisiert werden. Die Variable „Bildungsniveau“ xedu entspricht dem prozentualen Anteil an Bürgern, die einen ersten Hochschulabschluss besitzen (weiter unten LEVEL_4_EDU_PC). Die Variable „Wirtschaftskraft“ xeco (weiter unten PURCH_POWER_PE) enthält die durchschnittliche jährliche Kaufkraft pro Einwohner in Pfund. Die Variablen „Altersverteilung“ xage_young und xage_old enthalten schließlich den prozentualen Anteil der Einwohner zwischen 15 und 29 Jahren (weiter unten POP_15_29_PCT) bzw. der Einwohner, die älter als 60 Jahre sind (weiter unten POP_60__PCT), gemessen an der Gesamtbevölkerung. Diese Daten sind in der Attributtabelle des Layers festgehalten, der die Distrikte als Polygone enthält. Hierbei ist auf Vollständigkeit und einheitliche Formatierung zu achten. Alle im Folgenden verwendeten Daten liegen auf Distriktebene beim statistischen Bundesamt Großbritanniens vor, dem Office for National Statistics.
Hier die erste Hürde statistischer Analysen: Wie gut bildet meine Variable einen Zusammenhang aus der Realität ab? Entscheidend ist hierbei das richtige Verhältnis herzustellen, zwischen Komplexität, wie sie in der Realität vorliegt und Abstraktion, ohne die kein Modell funktioniert.
4 Schritte zum Erfolg mit OLS
Im nächsten Schritt verwende ich nun das Werkzeug Ordinary Least Squares (OLS). Dies sollte in jeder Regressionsanalyse der erste Schritt sein, zusammen mit der Ausgabe eines ausführlichen Report-Files, um sicher zu gehen, dass alle Vorrausetzungen für ein gültiges Modell erfüllt sind. Der nun folgende Qualitäts-Workflow ist für alle Analysen gleich. Er besteht in seiner Essenz aus 4 Fragen:
- Weist mein Modell nichtlineare Beziehungen zwischen den Variablen auf?
Ich überprüfe dies durch eine Darstellung meiner Variablen innerhalb eines Scatterplots (siehe Abb.2). Die Beziehungen sind linearer Natur, ich kann sie daher alle weiterhin verwenden.
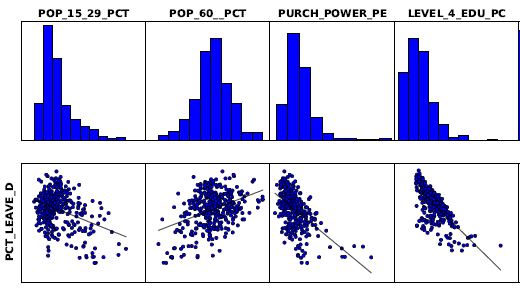
- Gibt es starke Ausreißer innerhalb der Variablenausprägungen?
Ich überprüfe ein zweites Mal die Darstellung innerhalb des Scatterplots und bemerke einige Ausreißer. Ich filtere diese heraus und lasse die Analyse ein weiteres Mal laufen. Die Qualität des Modells (AIC-Wert), generell je höher, desto besser) wird dadurch aber nicht merklich verbessert.
- Besteht Multikollinearität zwischen meinen unabhängigen Variablen?
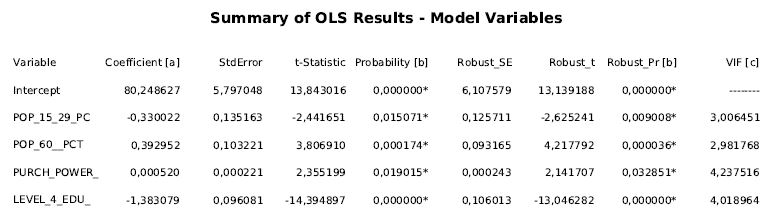
Multikollinearität führt zu einer Überbewertung von Variablen durch redundante Information. Zur Überprüfung betrachte ich den VIF-Wert, der für alle Variablen kleiner 7,5 sein sollte. Dies ist der Fall (siehe Abb.3).
- Fehlt eine entscheidende, unabhängige Variable in meinem Modell?
Diese Frage ist schwieriger zu beantworten. Ich betrachte zuerst den R²-Wert meines Modells, über den ich feststellen kann, wieviel Prozent der beobachteten Fälle durch meine Variablenkonstellation erklärt werden. Er liegt bei 0,56 (Die Spanne liegt zwischen 0 und 1). Für die Sozialwissenschaften ist das kein schlechter Wert, aber fast 50 Prozent der Varianz lässt sich noch nicht erklären – das ist noch unbefriedigend. Im nächsten Schritt lasse ich mir die Verteilung der Standardabweichung für Residuen auf der Karte anzeigen (siehe Abb.4).

Große Abweichungen ins Positive wie Negative belegen eine mangelhafte Erklärungskraft der Variablen in den blauen und roten Gebieten. Um den sehr unterschiedlichen Landesteilen mit ihren eigenen Landesregierungen Rechnung zu tragen, ergänze ich mein Modell um eine Dummy-Variable für Schottland, Wales und England. Ein erneuter Durchlauf des Modells erhöht den R²-Wert auf 0,69 bei einem p-Wert von kleiner 0,01. Die Wahrscheinlichkeit, dass dieser Zusammenhang rein zufälliger Natur ist, liegt also bei weniger als 1 Prozent. Die Tatsache, dass jemand in Schottland wohnt, hat neben den anderen unabhängigen Variablen einen statistisch signifikanten Einfluss auf sein Abstimmungsverhalten.
Welche Variable hat den größten Einfluss?
Nachdem diese vier diagnostischen Fragen zufriedenstellend geklärt sind, betrachte ich die Koeffizienten aus Abb.3. Den stärkten Einfluss hat das Bildungsniveau, wobei hier, erwartungsgemäß, eine negative Korrelation vorliegt. Je höher das Bildungsniveau, desto geringer war der Anteil der Bürger, die für den Austritt aus der EU stimmten. Die zweitwichtigste Variable war die Altersverteilung. Ein hoher Anteil an jungen Bürgern ließ die Zustimmung für den Austritt sinken (man beachte das negative Vorzeichen), wohingegen ein hoher Anteil an älteren Bürgern mit einem Zuspruch für den EU-Austritt korreliert. Nur eine geringe Bedeutung hat hingegen die Kaufkraft, die nur mit einem Wert von 0,0005 in die Berechnung mit einfließt. Unterschiede in der durchschnittlichen Kaufkraft pro Distrikt haben also zumindest in diesem Modell keine Auswirkungen auf das Abstimmungsverhalten.
Keine Ruhe lässt mir jedoch immer noch die starke Bedeutung der Dummy-Variablen und der rötliche Teilbereich im Osten Englands in Abb. 4. Ich entschließe mich daher sowohl eine weitere OLS-Analyse sowie eine gewichtete Regressionsanalyse nur für den Teilbereich England durchzuführen. Die OLS für England alleine erreicht einen R²-Wert von 0,87, was einerseits fabelhaft ist, andererseits zeigt der Test für räumliche Autokorrelation (verfügbar im Toolset „ Analyzing Patterns“) ein weiteres räumliches Cluster an Residuen. Etwas scheint mir zu entgehen, den Ergebnissen ist so nicht zu trauen. Ich will daher zumindest erfahren, wo meine Variablen innerhalb Englands die stärkste Einflusskraft haben.
GWR – Den Raum als Variable mit einbeziehen
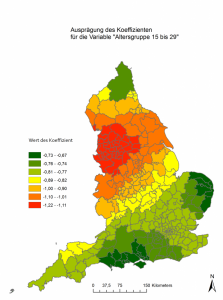
Hierfür wende ich eine geographisch gewichtete Regression an (GWR). Die Vorrausetzungen sind hierbei nochmals strenger als bei der OLS-Analyse, aufgrund von räumlicher Clusterung muss ich zwei Variablen aus dem Modell entfernen. Ich entscheide mich für die Kaufkraft, da deren Beitrag zum Modell generell geringer war und eine Variable, die für die Altersverteilung operationalisiert ist. Für jeden der Distrikte wird nun eine eigene Regressionsgerade aufgestellt. Die Verteilung der Koeffizienten für beide Variablen (siehe Abb. 5 und Abb.6) zeigen mir, in welchen Distrikten der Einfluss der jeweiligen Variablen größer ist. Es zeigt sich, dass im östlichen Cluster Englands gerade das Bildungsniveau einen hohen Eintrag in das Modell verzeichnet. Ein höherer Bildungsanteil in der Bevölkerung wirkt sich hier wesentlich stärker auf das Abstimmungsverhalten aus, als dies zum Beispiel im grünen Bereich um London der Fall ist.

Was bleibt als Fazit aus diesem kurzen Forschungsprojekt? Räumliche Regressionsanalysen sind ein mächtiges Werkzeug, wenn man darauf achtet, dass alle Anforderungen erfüllt sind. Es ist kein Werkzeug, bei welchem man einfach zwei, drei Knöpfe klickt und dann sofort eine Aussage in der Hand hält. Vielmehr bedarf es einer schrittweisen Anpassung des Modells mittels unterschiedlicher diagnostischer Tools. Im Falle Brexit haben sich die Hypothesen bezüglich Altersverteilung und Bildungsniveau bestätigt, wobei das Bildungsniveau eine größere Bedeutung hat als die Altersverteilung.
Weitere Einsatzfelder für räumliche Regressionen finden sich zum Beispiel in der Kriminalitätsbekämpfung, dem Gesundheitswesen und der Habitatsmodellierung im Bereich der Biologie.